| INTERVALOS |
Los intervalos numéricos en R son conjuntos de números reales y se representan mediante un segmento con o sin extremos. Pueden ser acotados o no acotados: Intervalos acotados:
|
Pulsa el botón inicio para generar un intervalo acotado. Con el control tipo puedes cambiar el tipo de intervalo. Si mueves el punto verde puedes ver los puntos que son del intervalo. Copia en tu cuaderno al menos dos ejemplos de cada tipo. |
Intervalos no acotados:<
|
Pulsa el botón inicio para generar un intervalo no acotado. Con el control tipo puedes cambiar el tipo de intervalo. Si mueves el punto verde puedes ver los puntos que son del intervalo. Copia en tu cuaderno al menos dos ejemplos de cada tipo. |
15. EJERCICIOS | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pulsa el botón EJERCICIO y se genera un ejercicio de intervalos. Te lo dan en forma analítica o en forma de intervalo y lo debes escribir en la forma de intervalo o analítica, respectivamente. Cuando lo hayas hecho pulsa el botón SOLUCIÓN para ver si lo has hecho bien. Si superas la prueba puedes seguir con la siguiente página Intervalo, si no la superas debes repetirla. Intervalo (matemáticas)Artículo de la Enciclopedia Libre Universal en Español.Los intervalos son los subconjuntos conexos de R. Más precisamente, son las únicas partes I de R que verifican la propiedad siguiente:Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados, semi abiertos, abiertos y cerrados) o según su características métricas (su longitud: nula, finita no nula, o infinita). Existen dos notaciones en España: [a; b) o [a; b[ para representar el conjunto de los x tal que a ≤ x < b. La primera es la vigente en el mundo anglosajón, la segunda en Francia y en la francofonía. La regla del corchete invertido resulta más intuitiva si uno se imagina que el corchete es una mano que tira hacia fuera o empuja hacia dentro, respectivamente, un extremo del intervalo. En el ejemplo anterior, a pertenece al intervalo mientrás que b no. Aquí están todos los casos posibles, con a ≤ b, y x perteneciente al intervalo, y l su longitud:
Si I = ]a, b[, su centro es Se nota De la misma manera, I = [a, b] corresponde a la condición |x - c| ≤ r. En tal caso se habla de bola cerrada. Se nota este conjunto: Tomemos I = [a, b] y J = [c, d]. Entonces a ≤ x ≤ b, y c ≤ y ≤ d. podemos sumar las inegualdades: a + c ≤ x + y ≤ b + d. Lo que justifica que I + J = [ a + c , b + d ]. Para la diferencia, hay que mirar primero - y : - d ≤ - y ≤ - c, y luego se puede sumar las desigualdades: a - d ≤ x - y ≤ b - d. De ahí obtenemos I - J = [ a - d, b - d ]. Si se toman a, b, c y d positivos no nulos, el producto y el cociente son también sencillos: I · J = [ ac, bd ] y I / J = [ a/d, b/c |
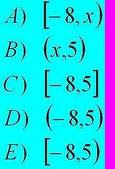





COPIAR EN EL PORTAFOLIO, EL CONTENIDO DE INTERVALOS, LUEGO DÁ TU PROPIAS IDEAS Y COMENTA CON TUS COMPAÑEROS.
ResponderEliminarES IMPORTANTE PRESENTARLO A LICDA, CATALINA DE MENDOZA, CUALES SON TUS RESULTADOS.
ESCRIBE ESTE BLOG EN TU PORTAFOLIO; COMENTA TUS IDEAS, ¿QUÉ ES UN INTERVALO?
ResponderEliminar