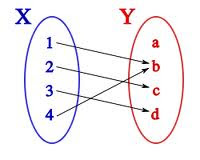
Una función es una regla de asociación que relaciona dos o mas conjuntos entre si; generalmente cuando tenemos la asociación dos conjuntos las función se define como una regla de asociación entre un conjunto llamado dominio con uno llamado codominio, también dominio e imagen respectivamente o dominio y rango. Esta regla de asociación no permite relacionar un mismo elemento del dominio con dos elementos del codominio.

Figura 1. Definición de función que se ampara bajo una regla de asociación de elementos del dominio con elementos del codominio, imponiendo la restricción de relacionar un elemento del dominio con uno del codominio, sin importar si los elementos del codominio puedan estar relacionados con dos o mas del codominio.
Donde se dice que f : A ® B (f es una función de A en B, o f es una función que toma elementos del dominio A y los aplica sobre otro llamado codominio B)
Se dice que el dominio de una función son todos los valores que puede tomar el conjunto del dominio y que encuentra correspondencia en el conjunto llamado codominio, generalmente cuando se habla del plano, el dominio es el intervalo de valores que están sobre el eje de las X´s y que nos generan una asociación en el eje de las Y´s.
El otro conjunto que interviene en la definición es el conjunto llamado codominio o rango de la función, en ocasiones llamado imagen, este conjunto es la gama de valores que puede tomar la función; en el caso del plano son todos los valores que puede tomar la función o valores en el eje de las Y´s.
También, cuando se grafica en el plano cartesiano se tiene una relación de dos variables, considerando como variable aquella literal que esta sujeta a los valores que puede tomar la otra.
Son aquellas variables que como su nombre lo indica, dependen del valor que toma las otras variables Por ejemplo: f(x)= x, y o f(x) es la variable dependiente ya que esta sujeta a los valores que se le subministre a x.
VARIABLE INDEPENDIENTE.
Es aquella variable que no depende de ninguna otra variable, en el ejemplo anterior la x es la variable independiente ya que la y es la que depende de los valores de x.
VARIABLE CONSTANTE.
Es aquella que no esta en función de ninguna variable y siempre tiene el mismo valor ejemplo:
Y=2, la constante gravitacional, entre otras.
La siguiente gráfica define una función, línea recta con pendiente (m = 1) que pasa por el origen, la cual es función debido a no existe un elemento del dominio que relaciones dos elementos del codominio. El dominio es (-¥, ¥) o lo que equivale a decir que el dominio toma todos los valores sobre la línea recta. El rango de la función o codominio es también el mismo, ya que toma todos los valores en el eje de las Y´s (-¥, ¥).
La expresión mediante la cual puede representarse esta ecuación es la siguiente:

Esta ecuación no tiene asociado dos elementos del codominio con uno del dominio, sin embargo la definición de función no impone ninguna restricción al respecto.
Podemos analizar que en este caso el domino es (-¥, ¥). Sin embargo, sabemos que el hecho de que la función sea f(x)=x2 conduce a que solo el recorrido de la función mande a valores positivos, y por tanto el rango de la función es [0, ¥)

La siguiente ecuación no es función y2 = x
Su gráfico es el siguiente:

Propiedades de una función
En este apartado vamos a estudiar las propiedades fundamentales de las funciones. Cada uno de los vínculos siguientes te lleva a la explicación de cada una de dichas propiedades:
Definición
Tengamos en cuenta que la expresión “ser función de” significa “depender de”. Por lo tanto, una función expresa una dependencia entre dos magnitudes (recordemos que una magnitud es aquella característica o cualidad de un objeto que se puede medir). Podemos entender una función como una máquina de transformación:















De manera intuitiva podemos decir que una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda. Posteriormente veremos que los números que son aceptados por la máquina compondrán el dominio de definición de la función y el conjunto de elementos de salida compondrán el recorrido de la función.
Ejemplos
1.- La ley que relaciona el valor del área de un cuadrado con la longitud de su lado es una función. Sabemos que la expresión que nos relacionas ambas variables es  .
.
Observa que dependiendo del valor del lado del cuadrado vamos a obtener distintos valores en el área del mismo. Así, aparece una variable que no depende de nada (variable independiente: la l) y otra que si depende de los valores elegidos en la l (variable independiente: la A). Puedes pues construir una tabla con algunos valores:
En esta función, el dominio será el conjunto de todos los números reales positivos pues el lado de un cuadrado nunca puede tener una medida negativa.
Su recorrido es también el conjunto de todos los números positivos pues un área no puede ser negativa. Además siempre existe un cuadrado que tenga por área cualquier número positivo (bastará construir un cuadrado cuyo lado sea la raíz cuadrada del área elegida). 2.- Cualquier expresión del tipo y=f(x) de las estudiadas en cursos anteriores representa una función real de variable real. Definición
Definimos función de x en y como toda aplicación (regla, criterio perfectamente definido), que a un número x (variable independiente), le hace corresponder un número y (y solo uno llamado variable dependiente).
De una manera más rigurosa: Definición
Se llama función real de variable real a toda aplicación f de un subconjunto no vacío S de R en R
Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable x recibe el nombre de variable independiente y la y o f(x) variable dependiente o imagen. Ejemplos
Calcula la imagen de los números 0, 1, 2, y 10 en las siguientes funciones: 
Definición
El subconjunto S de números reales que tienen imagen se llama Dominio de definición de la función f y se representa D(f). Nota
El dominio de una función puede estar limitado por: 1.- Por el propio significado y naturaleza del problema que representa. Ejemplos
A.- En el ejemplo estudiado que relacionaba el área de un cuadrado con su lado viste que el dominio lo formaban los números reales positivos.
La función que representa este problema es f(x)=x2 como ya vimos; de todos modos observa que en principio y atendiendo al aspecto analítico de la función no habría inconveniente en calcular la imagen de un número real negativo; por ejemplo, f(-8)=(-8)2=64.
Luego parece que el dominio podría ser todo R. En este ejemplo, el dominio viene determinado pues, por la propia naturaleza del problema que no admite lados de cuadrados negativos. B.- Con la sucesión de números reales (an)= (-n2+18)
(es una función: f(n)=(-n2+18) pasa algo parecido pues en principio no tenemos inconveniente en calcular la imagen de cualquier número real.
No obstante, la propia definición de sucesión nos hace considerar que solo son posibles las imágenes de números naturales. 2.- Por la expresión algebraica que define el criterio.
A la hora de estudiar la expresión que representa una función tendrás que tener en cuenta tres aspectos fundamentales:
1 El radicando de una raíz de índice par debe ser positivo.
2 Si se trata de una división, el divisor debe ser distinto de cero.
3 La función logaritmo solo admite valores mayores estrictos que cero. Ejemplos
Calcula el dominio de definición de las siguientes funciones:
1.- f(x)=1/2x2
En este caso, al no aparecer cocientes ni raíces ni logaritmos en los que intervenga la variable x, podemos calcular la imagen a cualquier número real. Por tanto D(f)=R 2.-
Como el radicando de una raíz de índice par debe ser positivo, debemos exigir:
3.-
Ahora tendremos que los puntos que no pertenecen al dominio son los que anulan al denominador. Veamos cuales son:
x-1=0 luego x=1 Por tanto el dominio de f serán todos los números reales menos el 1: D(f)=R\{1}
4.-
Tengo que exigir de nuevo:
Ejercicios
Calcula el dominio de las siguientes funciones:

Definición
La gráfica de la función f es el lugar geométrico de los puntos del plano cuyas coordenadas satisfacen la ecuación y=f(x) Ejemplos
1.- Hallar los puntos de la curva y=x2-5x+6 que pertenecen al eje de abscisas o al eje de ordenadas. 2.- Representar la gráfica de la función f de R en R dada por 
Sean dos funciones reales de variable real dadas por las expresiones:
y1 = f1(x) y y2 = f2(x).
Se llama función suma de ambas, a la función:
ys = y1+y2 = f1(x)+f2(x). Análogamente podemos definir la función diferencia como
yd = y1-y2 = f1(x)-f2(x) Propiedad
El dominio de definición de la función suma, y también el de la función diferencia será la intersección de los dominios de ambas funciones. Ejemplos
Calcula la función suma de las siguientes funciones con sus dominios respectivos:
1.- f1(x)=x2+1 f2(x)=-2x2+4
ys=y1+y2=x2+1-2x2+4=-x2+5.
Además, 2.-
2.- 
Nota:
Observa que el dominio de la función resultante solo sería toda la recta real salvo el cero, que no coincide con la intersección de los dominios. A pesar de esto no debes calcular el dominio trabajando con la función resultante sino con la intersección. Ejercicios
Calcula las funciones suma y diferencia de las siguientes funciones con sus dominios respectivos: 
Sean dos funciones reales de variable real dadas por las expresiones:
y1 = f1(x) y y = f2(x).
Se llama función producto de ambas, a la función:
yp = y1×y2 = f1(x)×f2(x). Análogamente podemos definir la función cociente como

Propiedad
Análogamente a lo que ocurre con las funciones suma y diferencia, el dominio de definición de estas funciones vuelve a ser la intersección de los dominios.
Pero además, en la función cociente, habrá que quitar todos los puntos que anulen a f2(x) puesto que serán puntos que anulen el denominador de dicha función. Ejemplos
1.- Dadas las funciones y1=x+1 y y2=x+2 calcula yp así como yc con sus dominios respectivos.

puesto que el -2 anulará el denominador de la función cociente.
2.- Idem con las siguientes funciones:

Observa que en la función cociente también hemos quitado del dominio el punto 1 puesto que la función y2 se anula para dicho punto. Ejercicios
Calcular yp así como yc en los siguientes casos:

Dadas dos funciones y=f(x), z=g(y), se llama función compuesta (gof) a la función (gof)(x)=g(f(x))

Observando este esquema observamos que para que exista la función compuesta es necesario que el recorrido de la función f quede totalmente incluido en el dominio de la función g. Nota
Si no se verificara esta condición podríamos construir una función compuesta realizando una restricción en los puntos donde no existen problemas. En este caso, el dominio de definición de la nueva función sería:
Dom(gof)=
Ejemplos
1.- Estudiar la existencia de la función compuesta de las siguientes funciones y en caso afirmativo calcularla: f(x)=x+1 g(x)=x2+1
En este caso el dominio de la función g es todo R. Cuando esto ocurra, la función compuesta existe y el dominio de la misma coincidirá con el dominio de f.
Por tanto, en este caso la función compuesta existe y Dom(gof)=Dom(f) = R
Además gof(x)=g(f(x))=(f(x))2+1=(x+1)2+1=x2+2x+1+1=x2+2x+2 2.- Estudiar la existencia de gof en el caso:
En este caso, Dom(g)=R luego el la función gof existe siendo además
Dom(gof)=Dom(f)=

3.-Dadas las funciones estudiar la existencia de gof y de fog
estudiar la existencia de gof y de fog
a)gof
Dom(g)=R\{0}. Por tanto, si existe algún punto del dominio de f tal que f(x)=0 entonces no existirá gof. Veámoslo:
 .
.
Por tanto, como existe un punto verificando eso, la función gof no existe en este caso. No obstante construyamos una restricción. Para ello bastará con quitar al dominio de f los puntos que verifican que f(x)=0.
Dom(f)=R\{-2} Y Dom(gof)=R\{-2,1}
b)fog
Dom(f)=R\{-2}.
Por tanto habrá que comprobar si existe algún punto tal que g(x)=-2:
 .
.
Como existe un punto en esas condiciones, no existe fog. No obstante construyamos una restricción. Para ello bastará con quitar al dominio de g los puntos que verifican que g(x)=-2.
Dom(g)=R\{0} Y Dom(gof)=R\{-1/5,0} Ejercicios
1.- Dadas las funciones f(x)=3x-7 y g(x)=2x+k, determinar k para que gof=fog. 2.- Dadas la funciones  , calcular si es posible la función gof.
, calcular si es posible la función gof.
3.- Dada la función , comprobar que (fofof)(x)=x
, comprobar que (fofof)(x)=x
4.- Estudia la función gof siendo f(x)=8x-3
5.- Estudiar las funciones gof y fog en el caso
Se llama función identidad a la función que le hace corresponder a cada número real el propio número. Se representa por I(x). Definición
Una función f se dice inyectiva o función uno a uno si verifica que dos puntos distintos no pueden tener la misma imagen. De otra forma: 
Ejercicios
1.-Comprobar analíticamente si las siguientes funciones son inyectivas o no:

Definición
Sea y=f(x) una función. Llamamos función inversa (en caso de que exista) a una función notada f-1(x) que verifica que (f-1of)(x)=I(x) con I(x) la función identidad.
Para que exista la función inversa de f es necesario que la función f sea inyectiva. Ejemplos
1.- Calcular si es posible la función inversa de  .
.
En primer lugar debemos estudiar si la función en cuestión es inyectiva o no:

Con esto queda probado que la función f es inyectiva y por tanto existe f -1. Calculémosla:

Ejercicios
1.- Calcular si es posible la función inversa de  . 2.- ¿Existe la función inversa de f(x)=x2?
. 2.- ¿Existe la función inversa de f(x)=x2?
3.- Dada la función f(x)=4x-6; se pide:
a) ¿Existe f -1?
b) calcular f -1
c) Calcular f -1(f(3)) y f(f -1(3))
4.- Dadas las funciones f(x)=x2+1 y g(x)=2x+4. Calcular sus inversas si es posible.



En las funciones, en lugar de introducir monstruos y sacar guaperas, introducimos números (con los que la función hace operaciones) y sacamos otros números:

Los números que obtengamos “al pasarlos” por la función dependerán de los que hayamos “metido”, al igual que el guaperas que obtenemos es función o depende del monstruíto que hayamos metido en la máquina de hacer guaperas. Los números que introducimos en la función se denominan valores de la variable x, los números que obtenemos se denominan valores de la variable y. Dado que los valores de la y son función o dependen de los valores de la x tenemos que la x es la variable independiente y que la y es la variable dependiente. Esta relación de dependencia se expresa con la notación
y=f(x) que se lee como “y igual a efe de x”
Definición de función
Se llama función a toda correspondencia o relación de dependencia que asocia a cada valor de la variable x un único valor de la variable y. Es decir cada valor de la variable x a través de la función tiene una única imagen o valor de la variable y.
Continuidad
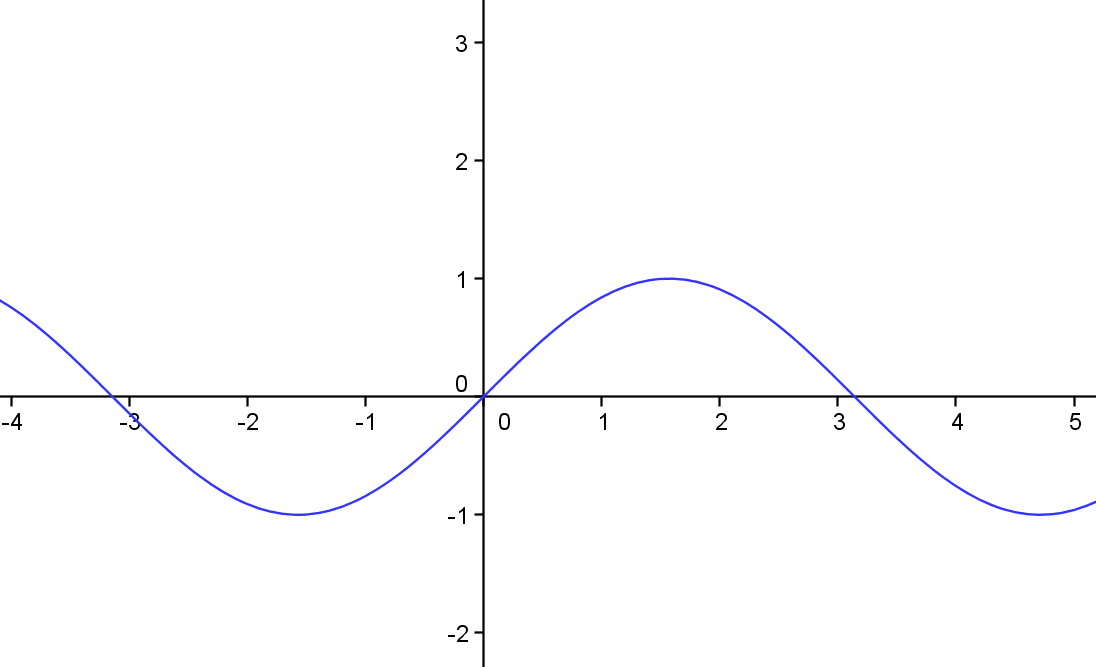
Si una función y=f(x) pude representarse en todo su dominio mediante un trazo continuo decimos que dicha función es continua. Es decir, si puedes dibujar la gráfica de la función sin levantar el lápiz dicha función es continua. Veamos a continuación la gráfica de una función continua:

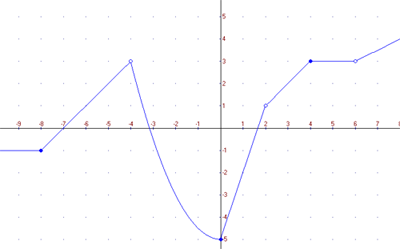
Cuando esto no ocurre, es decir, cuando tenemos que levantar el lápiz en algún momento a la hora de trazar la gráfica de la función, se dice que la función es discontinua. Puede ocurrir que una función sea discontinua en su dominio para determinados puntos. Observa el siguiente ejemplo:

Fíjate en los puntos que no tienen relleno. Esa es la forma de representar que la función no tiene dibujo exactamente ahí, o dicho matemáticamente, la función no existe o no está definida en ese punto. Así, la función del ejemplo no está definida para x=-4, x=2 y x=6. Por tanto, para dichas abscisas la función es discontinua, levantaríamos el lápiz a la hora de dibujar la gráfica justamente para dichos valores de la x.
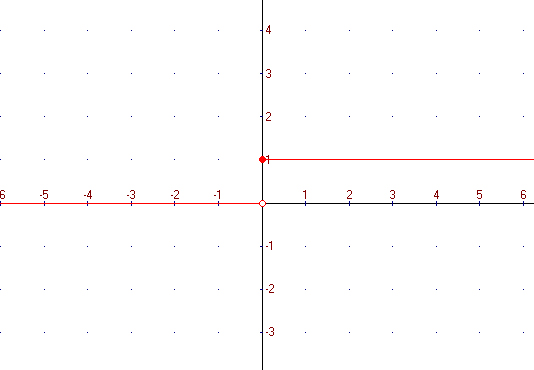
Puede ocurrir que la función sí exista o esté definida en un punto pero sea discontinua en el mismo, observa el siguiente ejemplo:

Cuando dibujo la función empezando por la izquierda, realizo un trazo continuo hasta llegar a x=0. Tengo que pegar un salto con el lápiz para seguir dibujándola, por lo tanto la función es discontinua en x=0. Pero observa que en x=0, en el trazo que empieza a la altura y=1, el punto está relleno, así que la función sí tiene dibujo o existe para x=0. Lo que nunca podría ocurrir es que los dos puntos se dibujaran rellenos, pues eso significaría que dicha gráfica no correspondería a una función, ya que a una misma x le corresponderían dos coordenadas y diferentes, lo que sabemos que va en contra de la definición de una función. Este tipo de discontinuidad se suele denominar "de salto".
Puede ocurrir que el salto sea infinito. Observa el siguiente ejemplo:

En esta función, para x=-2 vemos que cuando la función se acerca por la izquierda se dispara creciendo indefinidamente y muy rápido. Cuando nos acercamos a x=-2 por la derecha ocurre lo mismo, pero con la función disparándose hacia abajo, decreciendo indefinidamente y muy rápido. Parece que a la función "se le va la pinza" para esa abscisa. En cursos posteriores verás que la razón es que en x=-2 hay una asíntota. Pero no te preocupes, por ahora vamos a decir que en x=-2 hay "ramas infinitas" y que la función "se dispara hacia el infinito por la izquierda y hacia el menos infinito por la derecha en x=-2" . Además diremos que en x=-2 hay una discontinuidad de "salto infinito", mientras que la función presenta en x=0 una discontinuidad de "salto finito".
Si pinchas aquí podrás abrir una animación que te permite experimentar con la discontinuidad. Sigue las indicaciones, ¡es muy fácil!
Continuidad
Si una función y=f(x) pude representarse en todo su dominio mediante un trazo continuo decimos que dicha función es continua. Es decir, si puedes dibujar la gráfica de la función sin levantar el lápiz dicha función es continua. Veamos a continuación la gráfica de una función continua:

Cuando esto no ocurre, es decir, cuando tenemos que levantar el lápiz en algún momento a la hora de trazar la gráfica de la función, se dice que la función es discontinua. Puede ocurrir que una función sea discontinua en su dominio para determinados puntos. Observa el siguiente ejemplo:

Fíjate en los puntos que no tienen relleno. Esa es la forma de representar que la función no tiene dibujo exactamente ahí, o dicho matemáticamente, la función no existe o no está definida en ese punto. Así, la función del ejemplo no está definida para x=-4, x=2 y x=6. Por tanto, para dichas abscisas la función es discontinua, levantaríamos el lápiz a la hora de dibujar la gráfica justamente para dichos valores de la x.
Puede ocurrir que la función sí exista o esté definida en un punto pero sea discontinua en el mismo, observa el siguiente ejemplo:

Cuando dibujo la función empezando por la izquierda, realizo un trazo continuo hasta llegar a x=0. Tengo que pegar un salto con el lápiz para seguir dibujándola, por lo tanto la función es discontinua en x=0. Pero observa que en x=0, en el trazo que empieza a la altura y=1, el punto está relleno, así que la función sí tiene dibujo o existe para x=0. Lo que nunca podría ocurrir es que los dos puntos se dibujaran rellenos, pues eso significaría que dicha gráfica no correspondería a una función, ya que a una misma x le corresponderían dos coordenadas y diferentes, lo que sabemos que va en contra de la definición de una función. Este tipo de discontinuidad se suele denominar "de salto".
Puede ocurrir que el salto sea infinito. Observa el siguiente ejemplo:

En esta función, para x=-2 vemos que cuando la función se acerca por la izquierda se dispara creciendo indefinidamente y muy rápido. Cuando nos acercamos a x=-2 por la derecha ocurre lo mismo, pero con la función disparándose hacia abajo, decreciendo indefinidamente y muy rápido. Parece que a la función "se le va la pinza" para esa abscisa. En cursos posteriores verás que la razón es que en x=-2 hay una asíntota. Pero no te preocupes, por ahora vamos a decir que en x=-2 hay "ramas infinitas" y que la función "se dispara hacia el infinito por la izquierda y hacia el menos infinito por la derecha en x=-2" . Además diremos que en x=-2 hay una discontinuidad de "salto infinito", mientras que la función presenta en x=0 una discontinuidad de "salto finito".
Si pinchas aquí podrás abrir una animación que te permite experimentar con la discontinuidad. Sigue las ind
Continuidad
Si una función y=f(x) pude representarse en todo su dominio mediante un trazo continuo decimos que dicha función es continua. Es decir, si puedes dibujar la gráfica de la función sin levantar el lápiz dicha función es continua. Veamos a continuación la gráfica de una función continua:

Cuando esto no ocurre, es decir, cuando tenemos que levantar el lápiz en algún momento a la hora de trazar la gráfica de la función, se dice que la función es discontinua. Puede ocurrir que una función sea discontinua en su dominio para determinados puntos. Observa el siguiente ejemplo:

Fíjate en los puntos que no tienen relleno. Esa es la forma de representar que la función no tiene dibujo exactamente ahí, o dicho matemáticamente, la función no existe o no está definida en ese punto. Así, la función del ejemplo no está definida para x=-4, x=2 y x=6. Por tanto, para dichas abscisas la función es discontinua, levantaríamos el lápiz a la hora de dibujar la gráfica justamente para dichos valores de la x.
Puede ocurrir que la función sí exista o esté definida en un punto pero sea discontinua en el mismo, observa el siguiente ejemplo:

Cuando dibujo la función empezando por la izquierda, realizo un trazo continuo hasta llegar a x=0. Tengo que pegar un salto con el lápiz para seguir dibujándola, por lo tanto la función es discontinua en x=0. Pero observa que en x=0, en el trazo que empieza a la altura y=1, el punto está relleno, así que la función sí tiene dibujo o existe para x=0. Lo que nunca podría ocurrir es que los dos puntos se dibujaran rellenos, pues eso significaría que dicha gráfica no correspondería a una función, ya que a una misma x le corresponderían dos coordenadas y diferentes, lo que sabemos que va en contra de la definición de una función. Este tipo de discontinuidad se suele denominar "de salto".
Puede ocurrir que el salto sea infinito. Observa el siguiente ejemplo:

En esta función, para x=-2 vemos que cuando la función se acerca por la izquierda se dispara creciendo indefinidamente y muy rápido. Cuando nos acercamos a x=-2 por la derecha ocurre lo mismo, pero con la función disparándose hacia abajo, decreciendo indefinidamente y muy rápido. Parece que a la función "se le va la pinza" para esa abscisa. En cursos posteriores verás que la razón es que en x=-2 hay una asíntota. Pero no te preocupes, por ahora vamos a decir que en x=-2 hay "ramas infinitas" y que la función "se dispara hacia el infinito por la izquierda y hacia el menos infinito por la derecha en x=-2" . Además diremos que en x=-2 hay una discontinuidad de "salto infinito", mientras que la función presenta en x=0 una discontinuidad de "salto finito".
Si pinchas aquí podrás abrir una animación que te permite experimentar con la discontinuidad. Sigue las indicaciones, ¡es muy fácil!
1.- Definición de función.
Ejemplos
Observa que dependiendo del valor del lado del cuadrado vamos a obtener distintos valores en el área del mismo. Así, aparece una variable que no depende de nada (variable independiente: la l) y otra que si depende de los valores elegidos en la l (variable independiente: la A). Puedes pues construir una tabla con algunos valores:
l
|
A
|
1
|
1
|
2
|
4
|
10
|
100
|
1/2
|
1/4
|
0,5
|
0,25
|
Su recorrido es también el conjunto de todos los números positivos pues un área no puede ser negativa. Además siempre existe un cuadrado que tenga por área cualquier número positivo (bastará construir un cuadrado cuyo lado sea la raíz cuadrada del área elegida). 2.- Cualquier expresión del tipo y=f(x) de las estudiadas en cursos anteriores representa una función real de variable real.
De una manera más rigurosa:
Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable x recibe el nombre de variable independiente y la y o f(x) variable dependiente o imagen.

| Inicio de esta página | Página inicial | Ejercicios |
2.- Dominio de definición de una función.
La función que representa este problema es f(x)=x2 como ya vimos; de todos modos observa que en principio y atendiendo al aspecto analítico de la función no habría inconveniente en calcular la imagen de un número real negativo; por ejemplo, f(-8)=(-8)2=64.
Luego parece que el dominio podría ser todo R. En este ejemplo, el dominio viene determinado pues, por la propia naturaleza del problema que no admite lados de cuadrados negativos. B.- Con la sucesión de números reales (an)= (-n2+18)
(es una función: f(n)=(-n2+18) pasa algo parecido pues en principio no tenemos inconveniente en calcular la imagen de cualquier número real.
No obstante, la propia definición de sucesión nos hace considerar que solo son posibles las imágenes de números naturales.
A la hora de estudiar la expresión que representa una función tendrás que tener en cuenta tres aspectos fundamentales:
2 Si se trata de una división, el divisor debe ser distinto de cero.
3 La función logaritmo solo admite valores mayores estrictos que cero.
1.- f(x)=1/2x2
En este caso, al no aparecer cocientes ni raíces ni logaritmos en los que intervenga la variable x, podemos calcular la imagen a cualquier número real. Por tanto D(f)=R 2.-
Como el radicando de una raíz de índice par debe ser positivo, debemos exigir:
3.-
Ahora tendremos que los puntos que no pertenecen al dominio son los que anulan al denominador. Veamos cuales son:
x-1=0 luego x=1 Por tanto el dominio de f serán todos los números reales menos el 1: D(f)=R\{1}
4.-
Tengo que exigir de nuevo:

| Inicio de esta página | Página inicial | Ejercicios |
3.- Representación de funciones
| Inicio de esta página | Página inicial | Ejercicios |
4.- Operaciones con funciones
Suma de funciones.
Definicióny1 = f1(x) y y2 = f2(x).
Se llama función suma de ambas, a la función:
ys = y1+y2 = f1(x)+f2(x). Análogamente podemos definir la función diferencia como
yd = y1-y2 = f1(x)-f2(x)
1.- f1(x)=x2+1 f2(x)=-2x2+4
ys=y1+y2=x2+1-2x2+4=-x2+5.
Además,
 2.-
2.- 
Producto y cociente de funciones.
Definicióny1 = f1(x) y y = f2(x).
Se llama función producto de ambas, a la función:
yp = y1×y2 = f1(x)×f2(x). Análogamente podemos definir la función cociente como
Pero además, en la función cociente, habrá que quitar todos los puntos que anulen a f2(x) puesto que serán puntos que anulen el denominador de dicha función.

puesto que el -2 anulará el denominador de la función cociente.
2.- Idem con las siguientes funciones:

Observa que en la función cociente también hemos quitado del dominio el punto 1 puesto que la función y2 se anula para dicho punto.
Función compuesta.
Definición
Observando este esquema observamos que para que exista la función compuesta es necesario que el recorrido de la función f quede totalmente incluido en el dominio de la función g.
Dom(gof)=
En este caso el dominio de la función g es todo R. Cuando esto ocurra, la función compuesta existe y el dominio de la misma coincidirá con el dominio de f.
Por tanto, en este caso la función compuesta existe y Dom(gof)=Dom(f) = R
Además gof(x)=g(f(x))=(f(x))2+1=(x+1)2+1=x2+2x+1+1=x2+2x+2 2.- Estudiar la existencia de gof en el caso:
En este caso, Dom(g)=R luego el la función gof existe siendo además
Dom(gof)=Dom(f)=

3.-Dadas las funciones
a)gof
Por tanto, como existe un punto verificando eso, la función gof no existe en este caso. No obstante construyamos una restricción. Para ello bastará con quitar al dominio de f los puntos que verifican que f(x)=0.
Dom(f)=R\{-2} Y Dom(gof)=R\{-2,1}
Por tanto habrá que comprobar si existe algún punto tal que g(x)=-2:
Como existe un punto en esas condiciones, no existe fog. No obstante construyamos una restricción. Para ello bastará con quitar al dominio de g los puntos que verifican que g(x)=-2.
Dom(g)=R\{0} Y Dom(gof)=R\{-1/5,0}
3.- Dada la función
4.- Estudia la función gof siendo f(x)=8x-3
5.- Estudiar las funciones gof y fog en el caso
Función inversa.
DefiniciónPara que exista la función inversa de f es necesario que la función f sea inyectiva.
En primer lugar debemos estudiar si la función en cuestión es inyectiva o no:

Con esto queda probado que la función f es inyectiva y por tanto existe f -1. Calculémosla:

3.- Dada la función f(x)=4x-6; se pide:
b) calcular f -1
c) Calcular f -1(f(3)) y f(f -1(3))
4.- Dadas las funciones f(x)=x2+1 y g(x)=2x+4. Calcular sus inversas si es posible.





CADA TEMA COPIAR EN EL PORTAFOLIO.
ResponderEliminarUTILIZAR, LIBRO PARALELO, HACER SU PROPIO CONCEPTO.
COMPARTIR COMENTARIOS CON OTROS COMPAÑEROS
LEER ATENTO CADA CONTENIDO, COPIAR LO IMPORTANTE DE CADA TEMA.
ResponderEliminar